Enhancing Hi-C contact matrices for loop detection with Capricorn: a multiview diffusion model

Paper: Enhancing Hi-C contact matrices for loop detection with Capricorn: a multiview diffusion model

Introduction

High-throughput Chromosome Conformation Capture (Hi-C) technology has revolutionized our understanding of the 3D architecture of the genome.

However, a significant challenge in utilizing Hi-C data is its requirement for high-coverage sequencing to achieve the resolution necessary for detecting fine-scale chromatin structures, such as chromatin loops. High-coverage Hi-C datasets demand extensive sequencing efforts, making them costly and time-consuming to produce.

• According to Rao et al. 2014, a ideal resolution for hic matrix: 80% of loci have at least 1,000 contacts

Coverage is the primary factor influencing Hi-C resolution, meaning that resolution enhancement methods essentially predict high-coverage matrices at finer scales. This limitation has prompted the development of computational approaches aimed at enhancing the resolution of low-coverage Hi-C data, thereby enabling more detailed genomic analyses at reduced costs.

Problem Setting

For a set of experimental cell lines $C$, interaction frequency matrices are available for chromosomes $\Xi$.
In the supervised coverage enhancement task, we are given a dataset with $N$ pairs of low- and high-coverage contact matrices

$$D={\{(X_{\xi }^{(c)},Y_{\xi }^{(c)})\}}_{i=1}^N$$
for each cell line $c \in C$ and chromosome $\xi \in \Xi$.

The goal is to develop a model $f$ that approximates
$$Y_{\xi }^{(c)}\approx f(X_{\xi }^{(c)})$$
for all cell lines $c$ and chromosomes $\xi$. The model $f$ should also generalize well to new cell lines and different chromosomes.

Constraints

• The focus is on enhancing intrachromosomal contacts within a 2 Mb range.
• Each chromosome $\xi$ has $L_{\xi}$ total base pairs.
• Fixed resolution $\Delta$, resulting in contact matrix shapes of $L_{\xi}/\Delta \times L_{\xi}/\Delta$.
• The high-coverage version $Y^{(c)}_{\xi}$ contains $\gamma$-fold more contacts than its low-coverage counterpart.

Matrix Details

• Each entry $X^{(c)}_{\xi}[i, j]$ represents a $\Delta^2 = 10kb \times 10kb$ region of genomic interactions between the genomic regions $[10i \text{kb}, 10(i + 1) \text{kb})$ and $[10j \text{kb}, 10(j + 1) \text{kb})$, with $\Delta = 10 , \text{kb}$.
• For computational efficiency, the matrices are tiled into $40 \times 40$ non-overlapping submatrices $X^{(c)}_{\xi}[i : i + 40, j : j + 40]$, each covering a $400^2 \text{kb}$ region, aligning with existing Hi-C resolution enhancement frameworks.

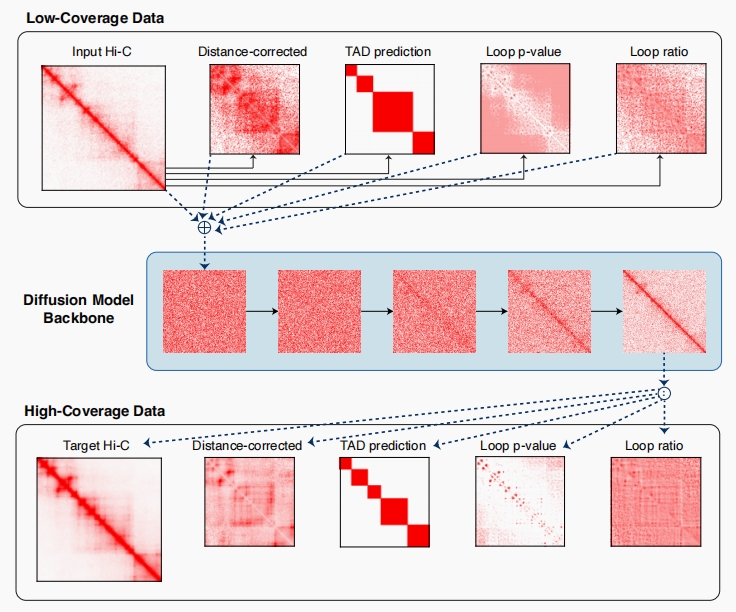
Capricorn Model Overview

Capricorn is designed to enhance the resolution of chromatin structures by explicitly modeling small-scale features such as loops and Topologically Associating Domains (TADs) leveraging a diffusion probability model as its backbone. By improving the interpretation of low-coverage contact matrices, Capricorn effectively identifies meaningful 3D chromatin interactions.

Methodology

Capricorn addresses the challenge of enhancing low-coverage Hi-C data by integrating small-scale chromatin features (such as TADs and loops) as additional inputs, alongside the primary Hi-C contact matrix. This multi-view approach allows Capricorn to generate high-resolution contact matrices that more accurately reflect the underlying biological structures.

Input Data Preparation:

In addition to the original matrix, we compute additional views of the paired $(X,Y)$ contact matrices using chromatin features derived from $X$ and $Y$.

• Distance-corrected matrices$(X^{(oe)},Y^{(oe)})$: Adjust for bias based on inter-locus distance, normalizing contacts based on expected distances to handle the diagonal dominance in the contact matrices. The expected matrix $E(X)$ is computed by averaging contacts along each diagonal, and the observed matrix is normalized accordingly.
• TAD scores$(X^{(tad)},Y^{(tad)})$: Utilize insulation scores (IS) (Crane et al. 2015) for TAD detection, identifying insulated regions with low scores and within-TAD regions with high scores.
• Loop p-value and ratio$(X^{(loop-p)},Y^{(loop-p)})$ and $(X^{(loop-r)},Y^{(loop-r)})$: Follow the Hi-C Computational Unbiased Peak Search (HiCCUPS) algorithm (Rao et al. 2014) for loop detection, assessing whether measured contacts are significantly more frequent than expected. This involves combining a 10x10 donut kernel with other kernels centered at a specific locus and computing the loop ratio and p-values based on a distance-based expected matrix. We incorporate HiCCUPS’s loop ratio and P-value as two additional views for each input contact matrix.

We compute these features directly from the low-coverage or high-coverage independently, so there is no data leakage, which would prevent Capricorn’s practical utility during inference. Finally, the full input and output are:

$$ \widetilde{X}(X) = [X, X^{(oe)}, X^{(tad)}, X^{(loop-p)}, X^{(loop-r)}] \in \mathbb{R}^{5 \times L/\Delta \times L/\Delta}$$
$$ \widetilde{Y}(Y) = [Y, Y^{(oe)}, Y^{(tad)}, Y^{(loop-p)}, Y^{(loop-r)}] \in \mathbb{R}^{5 \times L/\Delta \times L/\Delta}$$

Multiview weighting

Different biological views have varying value distributions, complicating accurate predictions. So we implement a two-stage iterative weighting process to normalize and refine the importance of each view:

• Initial Weights: Divide this standard deviation by the standard deviation of all other channels to obtain the initial weights $ \omega_0 \in \mathbb{R}^5 $. Mathematically, for each view $ i $: $ \omega_{0,i} = \frac{\sigma(X_i)}{\sigma_{\text{all}}}$. This normalization ensures that views with higher variability do not disproportionately influence the model.
• Refined Weights: Adjust weights using Mean Squared Error (MSE) loss from initial Capricorn runs to account for the difficulty of generating each view.
  Normalize these adjusted weights to obtain the final weights $ \omega \in \mathbb{R}^5 $: $\omega_i = \frac{\text{MSE}_i}{\sum \text{MSE}_j}$
  This normalization ensures that each weight accurately represents the relative importance and difficulty of its corresponding view.

Diffusion Model Backbone:

Capricorn leverages conditional diffusion probability models, treating the combined contact matrix and its derived chromatin feature views as a multi-channel image. We use the conditional diffusion probability model Imagen as the resolution enhancement backbone model, updating the model to condition on low-coverage contact matrices rather than text.

Training and Inference

During training, Capricorn learns to predict high-resolution contact matrices from their low-resolution counterparts and additional chromatin features. The objective is to minimize the Mean Squared Error (MSE) between the predicted matrices $ \hat{Y} $ and the ground truth high-resolution matrices $ Y $

During inference, Capricorn utilizes the trained diffusion model backbone along with the low-coverage contact matrix views to generate a high-coverage contact matrix estimate $ \hat{Y} $:

$$
\hat{Y} = f_\theta(\theta; \tilde{X}(X))
$$

Performance Measures

Capricorn’s performance is evaluated using both image-based and biologically motivated metrics. The model’s predicted high-coverage contact matrix is compared against the true high-coverage matrix using mean squared error (MSE) and loop F1 score.

The loop F1 score is calculated based on the number of correctly predicted loops, with a tolerance for positional discrepancies, to assess the model’s ability to accurately capture biologically relevant chromatin structures.

loop F1 score: $$ F1 = \frac{TP}{TP+\frac{1}{2}(FP+FN) } $$ with a 5 pixel (50kb) tolerance range.

• TP are the true positive loops called from the predicted data that appear within [i–5: i + 5, j–5: j + 5] in the loops called from the ground-truth data
• FP are the loops called from the predicted data that do not appear within the 5-pixel range from the ground-truth data
• FN are the loops that are called from the ground-truth data but do not occur in the five-pixel tolerance range for predicted data. We do not use true negatives in our evaluations.

Hi-C data preprocessing

1. Dataset: GM12878 Epstein-Barrvirus-infected human lymphoblastoid cell line and K562 human chronic myelogenous leukemia lymphoblast cell lines from the Rao et al. (2014) dataset (accession code GSE63525)
2. Preprocessing: Restricting the contact matrix to read mapping quality ≥ 30 and processed to 10 kilobase (kb) resolution, following previous work. We adopt the contact matrix preprocessing techniques from HiCARN and DeepHiC, including tiling the contact matrices into 40×40 submatrices, only retaining submatrices in the 2 megabase (Mb) region around the diagonal, clamping the high-coverage matrix to [0, 255] and then normalizing to [0, 1], and clamping the low-coverage matrix to [0, 100] and then normalizing to [0, 1].
3. Downsample: In order to simulate low-coverage data, we randomly downsampled the GM12878 and K562 cell line Hi-C matrices to 1/16 of the original read count.
4. We train on the GM12878 data and test the model on K562; in the second, we train on K562 data and test on GM12878. In both experiments, we withhold chromosomes 4, 5, 11, and 14 from the training cell line as our validation set.

Results

Capricorn accurately enhances contact matrices and loop features

Capricorn demonstrated remarkable performance in enhancing the resolution of Hi-C contact matrices and accurately identifying chromatin loops. Notably, it surpassed other models in enhancing chromatin loops and accuracy in generating high-coverage data.

In testing across GM12878 and K562 cell lines, Capricorn achieved an average loop F1-score improvement and significantly lower mean squared error (MSE) compared to other methods.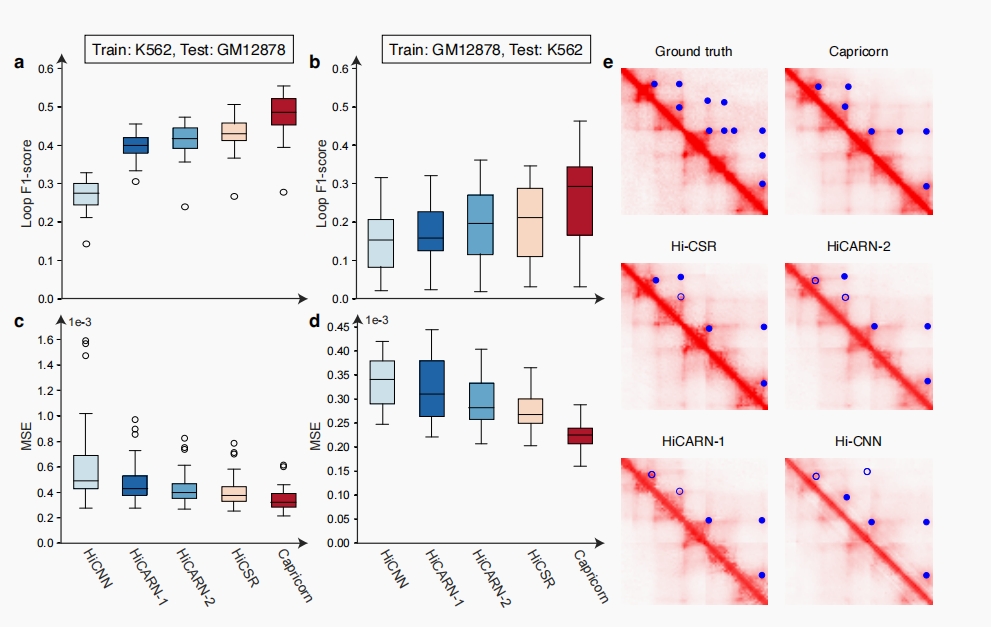

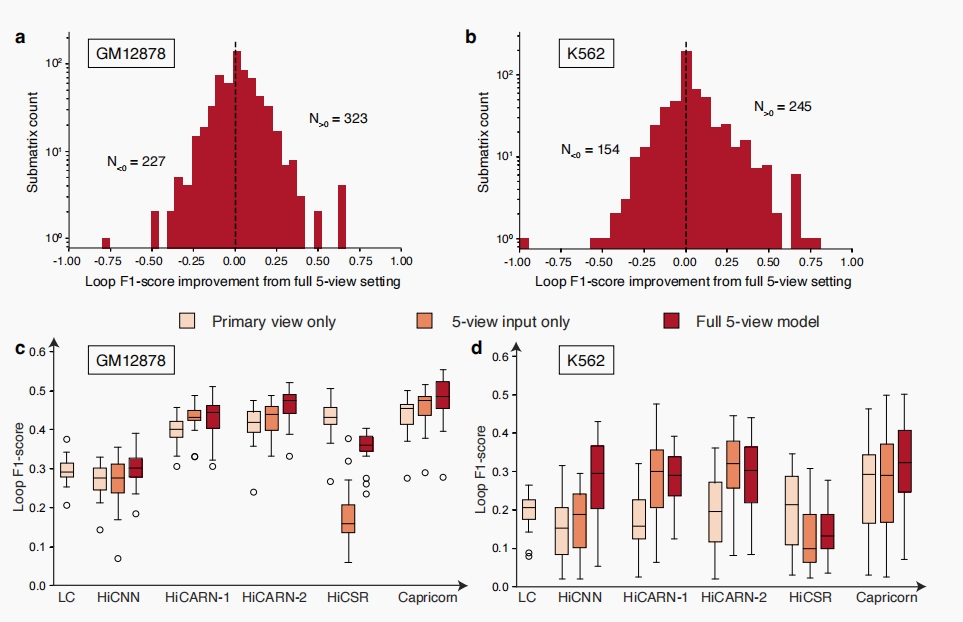
Small-scale chromatin features are critical to model improvement and are model-agnostic

Further analysis revealed that incorporating small-scale chromatin features (e.g., TADs and loops) as additional inputs significantly increased Capricorn’s performance. This approach not only improved the resolution enhancement task but also the model’s ability to identify structurally meaningful contacts from the enhanced matrices.

1. Primary view only: This setting uses the comparison models’ default resolution enhancement pipelines with the low- and high-coverage Hi-C matrices as input and output.
2. Five-view input only: This setting uses the additional chromatin feature views as input to the model, but is still trained to only predict the high-coverage view.
3. Full five-view model: This setting uses Capricorn’s complete multi-view setting, including all five chromatin feature views as input and training the model to enhance the small-scale chromatin features in addition to the Hi-C matrices.
   

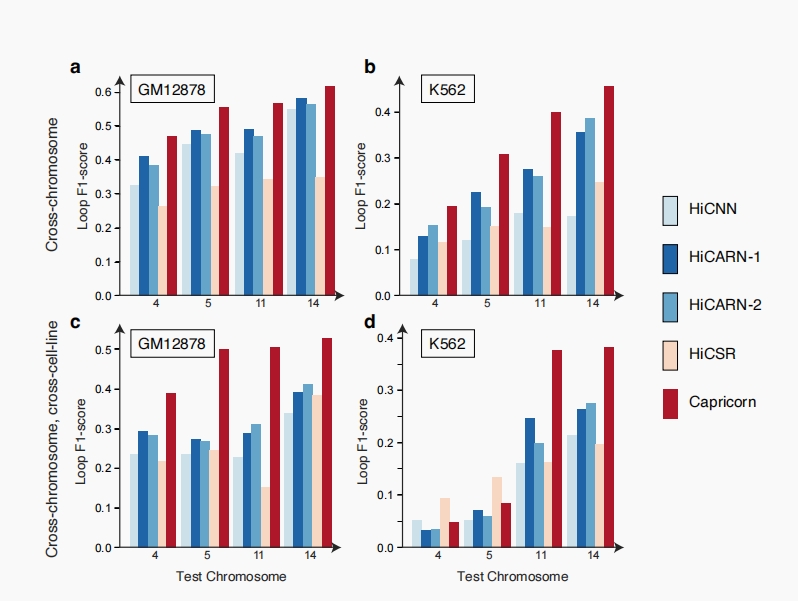
Capricorn generalizes across chromosomes

A rigorous testing regime confirmed Capricorn’s ability to generalize its learning across different chromosomes and cell lines, underscoring its robustness. The model effectively transferred learned patterns to new genomic loci, outperforming comparison approaches in identifying accurate chromatin loops, further evidenced by cross-chromosome and intra-cell-line generalizations.

Discussion and Future Directions

Capricorn represents a significant advancement in the field of Hi-C resolution enhancement by explicitly modeling the biological underpinnings of contact matrices through the incorporation of small-scale chromatin features. This approach has not only demonstrated Capricorn’s superiority in enhancing Hi-C data resolution but also highlighted its applicability to a broader range of resolution enhancement problems beyond its initial scope.

Future Directions

Looking forward, the Capricorn framework offers ample room for expansion to incorporate further biological views tailored to specific downstream applications. For instance, integrating structural information covering larger genomic loci could enhance the identification of TADs and A/B compartments, thereby broadening the model’s applicability and utility in genomic research.

Additionally, exploring the impact of varying model backbones on the multi-view resolution enhancement problem presents an intriguing avenue for future research. This could involve assessing the model’s adaptability to different genomic datasets, including those from other species, thereby extending its utility to a cross-species transfer learning context.

Moreover, applying Capricorn to a wider array of Hi-C cell line data and investigating the effects of training data size could yield insights into optimizing the model’s performance. Furthermore, the potential to adapt Capricorn for use with other types of contact map data, such as micro-C, suggests opportunities for broadening the model’s applicability within genomic research.

Lastly, future studies might explore the performance of Capricorn across various loop calling methods, enhancing the model’s capacity to accurately identify biologically relevant chromatin structures. This would not only solidify Capricorn’s standing as a robust tool for Hi-C resolution enhancement but also contribute to our understanding of the complex architecture of the genome.